The Genius and the Myth
He ranks with Archimedes, Euclid, Isaac Newton
and Leonard Euler as one of the greatest mathematicians of the world. He began
a new epoch in Indian astronomy and mathematics, that continued for more than a
millenium. His book Aryabhateeyam is
a masterpiece of brevity and eloquence.
But what did Aryabhata actually do? Aryabhata
did NOT invent zero; or gravity; or the heliocentric system. As I wrote in my
first essay, even Indian mathematics and Sanskrit scholars are stunningly
ignorant of Aryabhata’s actual accomplishments. Since we are equally ignorant
of almost all of ancient India’s glories, this is not specifically galling;
just generally abysmal. Only Bhaskara was perhaps as popular and admired, but
unlike Newton’s apple or Watt’s tea kettle, or the anecdotes of Birbal or
Tenali Raman, we don’t even have popular legends about him. But we are so
creative, we blame the British for this situation, decades after they left.
Ever computed a square root? Aryabhata.
Cube root? Aryabhata.
Summed up a series of numbers?
Aryabhata.
Series of squares? Aryabhata.
Divided by a fraction by multiplying by
its inverse? Aryabhata.
Computed the areas of triangles,
circles, trapeziums? Aryabhata.
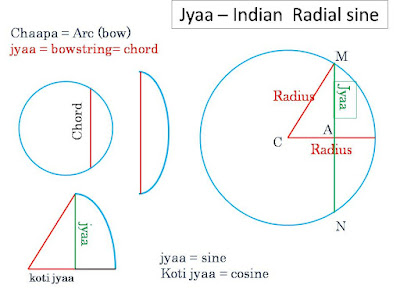
Calculated sines? Aryabhata.
And that’s just the simple mathematics we learn in school.
Wait! Did he invent ALL of these? Ah, that’s the question. Aryabhata himself claims not a single invention. He explicitly states that “by the grace of Brahma, the precious jewel of knowledge (jnana-uttama-ratnam) has been extracted from the sea of true and false knowledge (sat-asat-jnaana-samudraat), by the boat of my intellect (sva-mati-navaa).” As Euclid compiled five centuries of geometrical discoveries of the Greeks, Aryabhata compiled several centuries of mathematical and astronomical discoveries of Indians.
Sulba sutra and Jain mathematicians knew
how to compute, square roots, but Aryabhata was the first to describe the
algorithm. We don’t know if cube roots were calculated earlier, his algorithm
is the oldest extant. His sine calculations are considered much superior to
those listed by Varahamihira. His kuttakara
algorithm to find solutions is considered ingenious even today.
It is not feasible to explain his mathematical and astronomical discoveries in a magazine article for the general reader. There are excellent translations, technical papers, books that do that. This essay’s purpose is to provoke you to read them, and marvel at Aryabhata’s sva-mati-navaa. And to place Aryabhata and his work in historical context.
Manuja Grantham
The eighteen siddhantas were attributed to rishis. But every jyotisha siddhanta after Aryabhata and Varahamihira, is attributed only to men, not rishis. These arose from commenting, understanding, questioning, correcting, improving existing siddhantas and inventing or discovering new concepts. There was no fear or taboo against criticizing a mere manuja like Aryabhata or Bhaskara, rather than a rishi. This era of Mathematics and Astronomy is called “Classical” by historians. I prefer VarahaMihira’s phrase Manuja Grantha.
मुनिविरचितमिदमिति यच्चिरन्तनं साधु न मनुजग्रथितम् ।
तुल्येऽर्थेऽक्षरभेदादमन्त्रके का विशेषोक्तिः ॥१–३॥ – बृहत्संहिता
muni-viracitam-idam-iti yat-cirantanam
saadhu na manuja-grathitam
tulye-arthe-akshara-bhedaad-amantrake ko
viSheshokti – BrihatSamhita 1-3
Philosophically, this verse by Varahamihira, is as insightful and expressive as Kalidasa’s verse puraanamityeva na saadhu sarvam(Not everything is excellent, simply because it is ancient).
Aryabhateeyam
The phrase
Kusumapure abhyaarcitam gnaanam (knowledge respected in Kusumapura), in Aryabhateeyam hints that he lived in
Kusumapura (Pataliputra or Patna). No biography or portrait of any Indian
astronomer exists. The pictures of Aryabhata pervading the internet, as well as
his statue, are merely artists’ imaginations. Almost all we know about him
comes from his books and those of his critics and commentators, like
Brahmagupta and Bhaskara I, who mentions Pandurangasvami, Latadeva and
Nishanku, as pupils of Arybhata.
He composed:
(1) Aryabhateeyam
in 499AD when he was 23 years old. Multiple copies survive in full form.
(2) Aryabhata Siddhanta, which is lost, and known only by quotations from commentators. In this book, Arybhata advocated midnight as the starting hour of each day, instead of sunrise, perhaps based on Surya or Romaka Siddhanta. Aryabhateeyam uses sunrise as day-beginning.
I confine this essay to Aryabhateeyam. It consists of two parts.
The first, Dasha Geetika (Ten Songs),
lists astronomical constants:
·
Orbital periods and Diameters
of Sun, Moon, Planets
· Number of years in a yuga,
yugas in a kalpa, kalpas in a manu
·
Deviation of planets from the
ecliptic
·
Epicycles, in different
quadrants
·
Table of Sine differences.
His first verse is a salutation to Brahma - he
was a scientist, but not an atheist. Almost every jyotisha who followed him
begins his work with a salutation to his favorite God. Jain mathematician
Mahavira begins with an invocation to his namesake, the tirthankara Vardhamana
Mahavira. It may also indicate that he was updating the Paitamaha (Brahma) siddhanta, some of whose data, had become
obsolete.
The second part, called AryaAshataShatam (i.e The 108 Arya verses) consits of three
chapters – Ganita (Mathematics), Kaala Kriyaa (Calculating Time), and Gola (Sphere – i.e. Celestial, Sphere
meaning the visible universe).
The siddhantas of later jyotishas were each
nearly a thousand verses long. What Aryabhata summaries in one or two verses is
explained by them with whole chapters. So cryptic and compact was
Aryabhateeyam, it was impossible to understand without bhashyaas
(commentaries); such was its impact, that bhaashyaas were written on it
centuries after others improved upon his methods. Telugu Marathi and Malayalam
commentaries followed those in Sanskrit, Arabic etc; and English translations
in the colonial period, which range in appreciation from astonishment to incredulity
to calumny.
1. Ganita - Mathematics
The mathematics set forth by Aryabhata is mostly
practical, not theoretical: its primary purpose is astronomy. I mention only simpler
concepts in this essay.
It also varies from extremely simple to
extremely complex statements, hypotheses, and algorithms.
We must understand that mathematics was not
taught to school children, then as it is today; it was perhaps the most
advanced of technical subjects and confined to specialists. Arithmetic symbols familiar to us like + - x ÷ = were only introduced in
fifteenth century Europe. Mathematics was not expressed in equations, but in
slokas.
Aryabhata gives two line slokas like this:
त्रिभुजस्य फल शरीरं समदलकोटी भुजार्ध संवर्गः
Tribhujasya
phala shareeram samadalakoti bhujaardha samvargaH.
Translation “Multiplication (SamvargaH) of perpendicular(Samadalakoti) and half (ardha) the base(Bhuja) results (phala) in Triangle’s (Tribhuja-sya) area(Shareeram).”
A similar verse(sloka) defines the area of a circle as its half-perimeter (or half-circumference) multiplied by its half-diameter (radius)
This is a simple algorithm, just a formula really, to calculate one
value, based on known parameters. A more complex version is his algorithm for
summation of a series, which includes several calculations, including for the
mean of the series, and encoding an alternate algorithm! This way of stating
multiple mathematical formulae is called muktaka
by Bhaskara I.
Kaalakriyaa
– Time
Aryabhata divided time and circles with the same geometric units as earlier
siddhantas. His major departure, was to define the four yugapadas namely krta,
treta, dvaapara and kali, as of equal time; and as the time it took all the
nine planets to align, or complete an integral number of revolutions around the
earth. He included a biographical note, that 3600 years passed between the
beginning of Kali yuga (end of Mahabharata war) and the twenty-third year of
his birth. This implies that the constants in DashaGitike were based on his
personal observations in that year.
This differed from the smriti definition of the first three yugapadas as four, three and two times as long as the kaliyuga, and offended the orthodox of everyone. Even his followers didn’t accept this division, but they followed his computations and algorithms, as they were significantly better than those of earlier siddhantas.
Gola –
Celestial Sphere
Arybahata states that Solar and Lunar eclipses
are shadows of the Moon on Earth and Earth on the Moon, respectively. He also
stated that the Sun is the only source
of light, and not just planets, but even the stars only reflect sunlight.
 |
| Kadamba flower |
Aryabhata used the metaphor of a kadamba-pushpa-grantha, to explain how people and creatures in all
parts of the world believe they are standing on top of the world. He introduced
another metaphor, for Earth’s rotation: consider a boat-rider on the Ganga, who
feels trees on the shore pass him by; whereas, in reality it is the boat that
is moving. Similarly Aryabhata suggested, the earth actually rotates, and like
trees on a river bank, the stars seem to revolve around it. But it was only a
metaphor, not a proof.
He also explains such concepts as Ascencions of
the Zodiac, Sine of Ecliptic etc. which are too technical for this essay.
The impact of Aryabhata was phenomenal. Even
fervent critics could not ignore him or his works. But he launched an era of
manuja grantham, and he was followed by a long line of brilliant scholars, whom
we will discuss next.
-----------
This essay was first published as part of a series in Swarajya
For the entire series click this link --> Indian Astronomy and Mathematics
References
1.
The Aryabhateeyam by Walter Eugene
Clark, University of Chicago, 1930.
2.
Aryabhatiyam, translated by KV Sarma
and KC Sukla, Indian National Science Academy, New Delhi, 1976.
3.
Facets of Indian Astronomy, KV Sarma, Madras.