Era of Rishi Siddhantas

 Rishi Siddhaantas and Manuja Siddhaantas

The thousand years before Aryabhata were as rich in intellectual fervour and activity as the thousand years after him. This was the era of the composition of most of the Vedaangas, the creation of such seminal works like Bharata’s NaatyaShaastra, Chanakya’s ArthaShaastra, Vatsyayana’s KaamaSutra, and several magnificent treatises on various subjects. Among these were eighteen jyotisha siddhantas, all attributed to deva-s like Surya or rishi-s like Kashyapa, Atri, Mareechi as described in this sloka.

सूर्यः पितामहो व्यासो वसिष्ठोऽत्रि पराशरः ।
कश्यपो नारदो गर्गो मरीचिर्मनुरङ्गिराः।।
लोमशः पौलिशश्चैव च्यवनो यवनो भृगुः ।
शौनकोऽष्टादशश्चैते ज्योतिःशास्त्र प्रवर्तकः ।।

Surya pitaamaho vyaaso vashishto atri paraasharaH
Kashyapo naarado gargo mareechi-r manu-r angiraaH
lomashaH paulisha-shcaiva chyavano yavano bhrguH
shaunako ashtadasha-shchaite jyoti shaastra pravartakaH 

This stands in stark contrast with the Siddhantas in the post-Aryabhata classical era, all of which are ascribed to scholarly astronomers, but not rishis. Varahamihira’s phrase manuja-grantham, succinctly describes this.

This was the period during which numerals, the place value system, angular units like degrees, minutes and seconds, trigonometry, and several such mathematical concepts must have been discovered. Instruments like shanku (gnomon), chakra (hoop), gola (armillary sphere), ghati yantra (copper pot) were used.

But all 18 siddhantas are now lost, except the Surya Siddhanta, which was modified and updated in the later centuries. Fortunately, Varahamihira, a contemporary of Aryabhata, wrote a treatise called Pancha Siddhantika, a comparative study of five of these eighteen siddhantas. He quoted and explained several verses from them. So, we understand some concepts of the era.

Types of Jyotisha texts

Jyotisha texts come in several categories. Siddanta-s are once in a century grand texts, composed by superlative scholars. A siddhanta may have several commentaries, called bhashya-s, in the succeeding centuries. For practical use, more compact books called karana-s were composed, which was used by pandits to prepare almanacs/calendars called panchaanga-s for public use. The latter tradition is still extant.

It is my belief that the various texts on astronomy and mathematics rival the commentaries and compositions on the Ramayana and Mahabharata. So rich and so widespread was the literature.

Pancha Siddhantika

The five siddhantas Varahamihira studied, those of Pitamaha (Brahma),  Vashishta, Surya, Romaka and Paulisha, explain motions of planets (in a geocentric model), prediction of eclipses, sine tables, celestial longitudes and latitudes. None of these are mentioned in Vedanga Jyotisha. They vary mostly in minor details, which Varahamihira explains. The small Vedic yuga of five years was dropped, and the humongous yuga of 432000 years used. We have no idea when or how this changed. A day count, ahargana, counting number of solar days (regardless of month or year) since the start of the Kaliyuga, which began when the Mahabharata war ended, came into vogue. Kaliyuga years are found inscribed in several royal inscriptions; for example, the Anamalai inscription of Maranjadayan Varaguna Pandyan in Madurai.

The solar zodiac is used extensively. It was most probably borrowed from the Greeks or Babylonians. The solar zodiac is a popualar theme on ceiling sculptures of temples in Tamilnadu, like this one in Kudumiyan Malai, Pudukottai.

Romaka (also called Lomasha) and Yavana refer to a Roman and a Greek, Paulisha to a Paulus Alexandrinus, say historians of science. While some foreign ideas were obviously borrowed, there is a puzzling absence of inclusion of other ideas, including those of Euclid, Ptolemy, or Archimedes. Whereas the Greeks developed an epicyclic theory of planetary motion, Indians developed a theory based on air strings pulling the planets. Geometrically, these are simply different epicyclic model than those used by the Greeks. They involved extremely complicated geometry, trigonometry and algebra, but they were quite accurate in predicting eclipses, solar and lunar, the biggest challenges of Indian astronomy.

That Mercury and Venus had a different type of orbital movement, from the other planets, Mars Jupiter and Saturn, was realized. Siddhantas explain eight types of planetary movement.

A vocabulary of scientific and technical words developed, to describe both such astronomical concepts and mathematical ideas and theorems.

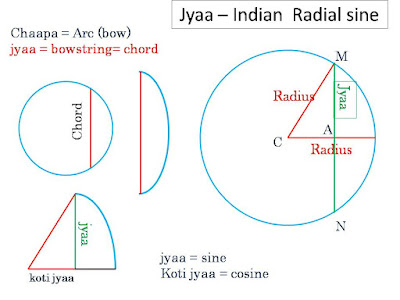
From the earlier knowledge of hypotenuses and circles, as found in Sulba Sutras, we can understand that the concepts of sine, cosine and other trigonometric ideas arose. The Indian sine was not the opposite/hypotenuse that we learn in school today, but the radial sine (abbreviated as R-sine), called the ardha-jyaa (half-bowstring). A chord connecting the ends of an arc looks like a bow (Sanskrit: chaapa or dhanush). When seen as part of a circle, the radius of the circle (CM )is the hypotenuse of the triangle (CMA) formed by the half-chord (MA), the radius touching the top (M) of this chord, and the segment (CA) of the radius dividing the chord into two equal halves. In Indian siddhantas, in the table of sines, expressed as a series, only the numerators are listed. Hence they are radial sines (multiplied by radius). The word for cosine is koti-jyaa.

The word jyaa and this concept of trigonometry traveled from India to Baghdad in the eighth century during the reign of Caliph al-Mamun, along with the zero, the decimal place value system, Indian numerals (now called Arabic numerals) and the works of Aryabhata and Brahmagupta. It transformed into the Arabic word jyaab or jeyb which means pocket. This then was taken to Europe by Leonardo Fibonacci, an Italian merchant, in the twelfth century, and translated into Latin as sinus, and later into English as sine. Then it came to India under English colonialism, making a full circle (pardon the pun) into our mathematical textbooks as sine. We learn trigonometry as the gift of the Europeans, not realizing its Indian origin.

Angular measurements called kalaa (degrees) liptaa (minutes) and viliptaa (seconds), were used, based on the sexagesimal system (Base-60) rather than decimal, which hints at a Babylonian origin. In addition, a sub division of the second into sixty parts and division of the cirlce into twelve parts (called raashi) also existed. Angles were often represented in karana texts with five aspects, not just the three we use today.

The division of time was also sexagesimal, with a day consisting of sixty naadis, each naadi of sixty vinaadis. Remember, the naadi existed in the Vedic period; was it indigienous or imported? It’s not one of several mysteries.

Step by step mathematical procedures (now called algorithms, after the Uzbek mathematician, Mohammad ibn Musa al-Khwarezmi) also emerged in the era of 18 Siddhantas. The place value system and zero were invaluable in developing algorithms for multiplication and division, square and cube roots, and several algebraic procedures solving indeterminate linear equations.

Ujjain Meridian

Two millennia before the world adopted the Greenwich meridian, Indian astronomers used the Ujjain meridian, as the prime meridian of longitude in India. This is the longitude that passed from north pole (Meru) to south pole (Vadavamukha). That the earth was a globe, not a flat plain was well understood by astronomers. They believed that Devas lived at Meru and Asuras at Vadavamukha, and Mankind in between.

गगनमुपैति शिखिशिखा क्षिप्तमपि क्षितिमुपैति गुरु किञ्चित् ।
यद्वदिह मानवानामसुराणां तद्वदेवाधः ॥ १३– ४ ॥  Pancha Siddhantika 13-4

Gaganam-upaiti shikhi-shikaa kshiptam-api kshitim-upaiti guru kincit
Yadvad-iha maanavaanaam-asuraaNaam tadvadeva-adaH 

The flame (shikhaa) of a lamp(shikhi) points skywards (gaganam) and a heavy (guru) object (kincit) thrown (kshiptam) skywards falls back to earth (kshiti); this happens in the lands of men (maanavaanaam) and asuras (asuraaNaam)

This was one concept of gravity, before Newton changed it.

उदयो यो लङ्कायां सोऽस्तमयः सवितुरेव सिद्धपुरे ।
मध्याह्नो यमकोट्यां रोमक विषयेऽर्धरात्रं स॥ Pancha Siddhantika 15-23

Udayo yo lankaayaam sa-astamaya savitur-eva siddhapure
Madhyaahno yamakotyaam romaka-vishaye arddha-raatram saH

Translation When it is Sunrise (udaya) in Lanka, it is Sunset (astamaya) in Siddhapura, Noon (madhyaahna) at Yamakoti,  Midnight (arddha-raatra) in Romaka-vishaya 

Lanka is not the Sri Lanka we know, but the point where the Ujjain meridian intersects the equator. Ujjain was a major center of learning in ancient India, and is also perhaps closes to the Tropic of Cancer (Karkata). We don’t know what places Yamakoti and Siddhapura signify, perhaps they are also place marker names like the equatorial Lanka.

While all the other Siddhantas determine time with Ujjain as the prime meridian, Romaka Siddhanta says the days starts with sunset at Yavanapura, which is not Athens or Rome, but Alexandria in Egypt.

The logical thought process which inspired the use of Ujjain and Lanka for calculations is simple, but brilliant. Longitude and latitude determine local time. So, the times of sunrise, sunset, moonrise, eclipses, will vary from place to place. Once the calculations are made for a prime meridian like Ujjain, local panchaangam-s can be prepared with only minor changes applied for local longitude and latitude – these are called deshantara, Each Siddhanta has a section about it. 

Celestial longitudes and latitudes were easier to calculate, than those on earth. The Surya Siddhanta lists Rohitaka (Rohtak, Haryana) and Kurukshetra and other cities on the Ujjain meridian. Others list such places as Kanyakumari, Malavanagar, Sthaneshvar, Vatsyagulma, Mahishmati, Vananagara as cities on the Ujjain meridian.

Some  trivia : Ujjain passed on its torch to Madras, briefly. Today, Indian standard time is set on longitude 82.5E,  based on Greenwich meridian. But for about a century, the Madras meridian was used as the prime meridian, especially for railway clocks.

For the entire series click this link --> Indian Astronomy and Mathematics   

References

1.      Surya Siddhanta, by Phanindralal Gangooly

2.      Pancha Siddhantika, edited by KV Sarma

3.      Pancha Siddhantika, edited by G Thibaut, Sudhakara Dwivedi

Varahamihira's Gravity and Sphericity

In the Vedic era preceding the Era of the 18 Siddhantas, the earth was thought to be flat. The Puranas and Smritis mention a mountain Meru, sacred and gigantic, in the middle of the earth. Deva Loka was on top of this mountain, the Devas lived on it. Asuras lived beneath our world, in Naraka Loka or Paatala Loka, also called Vadavaamukha. Meru was surrounded by four continents, Kuru to the north, Bhadrashva to the east, Bharata to the south and Ketumala to the west.

Not only Hindus, but Buddhists and Jains also seem to have accepted this concept. In their religions also, Indra, Brahma etc are significant divine beings, who live on Meru, which is an immense sacred mountain.

Meru and continents

The belief is also captured in a beautiful verse in the Tamil epic, Silappadikaaram:

ஞாயிறு போற்றுதும் ஞாயிறு போற்றுதும்
காவிரி நாடன் திகிரிபோல்
பொன்கோட்டு மேரு வலம் வருதலான்.
 “nyaayiRu poTruthum, nyaayiRu poTrudum,
kaaviri naaDan tigiripol pon koTTu meru valam varudalaan.” 

Translation Salutations (potrudhum) to the Sun (nyaayiRu); who goes around (valam varudalaan) golden mountain (pon koTu) Meru, like the wheel (tigiri) of the Chola (“kaaviri naaDan”, Lord of Kaveri country).

Gola - Earth as Sphere

At some unknown time, astronomers across the world realized that the earth was a sphere. They also realized that the sky was different from the space beyond it, and sky and space were also spheres. Perhaps an individual proposed it; perhaps a group of people discovered it and discussed the idea and it spread. What literature survives doesn’t mention this historical discovery or its acceptance. The astronomical texts referred to earth as BhuGola (Bhu is Earth; Gola means sphere). The sky (kha) was thence called KhaGola; and the realm of stars (Bha) beyond it, BhaGola.

The astronomers of this period seemed to not bothered to refute the earlier flat-earth model, but simply remapped some aspects to their new understanding. So they called or redefined Meru as the North pole of  the spherical earth (still considered DevaLoka, Abode of the Devas) and Vadavamukha as South pole (abode of the Asuras).

The spherical earth presented a new conceptual challenge. What did the earth stand on? If the earth were a sphere, how did people not fall off the sides of the sphere? How did people or animals stay put on the lower half? Would they be upside down? A similar ideological challenge must have affected Greek and Chinese astronomers. Not until Newton in the 17^th century, was the concept of gravity proposed to explain planetary motion. This gravity was explained as a property of mass, though why it was so, could not be explained even by Newton. A generation before Newton, the French philosopher Rene Descartes proposed a vortex based theory of gravity. Newton’s theory became the accepted one, until Einstein’s relativistic theory of gravity overturned it.

Indian astronomers explained this away with metaphors.

Aryabhata compared the spherical earth with a kadama flower, which has a spherical centre. The buds, of a kadamba flower point outwards and their stalks point inwards; similarly explained Aryabhata, the legs of men and land animals and sea creatures point inward (toward the centre of the earth) and their heads point outward (towards the sky).

kadamba pushpa

Varahamihira used two better metaphors. The spherical earth is surrounded by a cage of stars, he said, inspiring a vision of a bird in a spherical metal cage. The earth is able to float in space, like an iron (loha) ball between two magnets (kantha), he continued. This is a scientific explanation with metaphors using common objects of his time.

पञ्च महाभूतमयस् तारागण पञ्चरे मही गोलः
खेऽयस् कान्तान्तः स्थो लोह इवा वस्थितो वृत्तः ॥ १३–१ ॥
Panchamahaa bhutam ayas taaragaNa panchare mahee golaH
Khe ayas kaanta-antaH stho loha ivaa vastitho vruttaH
 

Translation Composed of five elements(pancha mahaa bhutam), among the cage (panchara) of stars(taara), stands (stoh) the earth(mahee), as a globe(golaH), like (iva) a ball of iron (loha) between magnets (kaanta-antaH)

Cage of Stars - Taara gana panchara

Varahamihira added that like a lamp’s flame always points skywards, and any object thrown upwards falls to earth, people also walk about on earth with their heads skywards and feet on the ground.

गगनमुपैति शिखिशिखा क्षिप्तमपि क्षितिमुपैति गुरु किञ्चित् ।
यद्वदिह मानवानामसुराणां तद्वदेवाधः ॥ १३– ४ ॥  Pancha Siddhantika 13-4 ॥
gaganam-upaiti shikhi-shikaa kshiptam-api kshitim-upaiti guru kincit
yadvad-iha maanavaanaam-asuraaNaam tadvadeva-adaH
 

Translation The flame (shikhaa) of a lamp(shikhi) points skywards (gaganam) and a heavy (guru) object (kincit) thrown (kshiptam) skywards falls back to earth (kshiti); this happens in the lands of men (maanavaanaam) and asuras (asuraaNaam)

This is as close as we get to an Indian theory of Gravity from Varahamihira – that heavy things fall to earth naturally. 

Newton’s concept gravity is much more ingenious and bold : it is not about planets but all objects: a brick exerts gravity on another brick, a tree on another tree, and of course celestial bodies on each other. But such a concept was not proposed by anyone before Newton, even Galileo or Copernicus or Kepler, leave alone the ancient Greeks like Euclid or Ptolemy.

Both Aryabhata and Varahamihira then quipped that Devas living on the north pole (Meru) and Asuras on the south pole (Vadavamukha) considered the other group as beneath them, punning on geography and social status. 

Whether the general public accepted these explanations or even heard of them is doubtful. Artists continued to depict the earth as a lady, Bhudevi in sculpture and painting, and her worship went on as usual. No one went on pilgrimages to Meru.

The Surya Siddhanta, composed unknown centuries before Aryabhata and Varahamihira, doesn’t even explain such matters. It talks about spherical earth, its longitudes and latitudes, the equator, gives the diameter of the sun and moon, explains calculations of their speed of revolution around the earth, uses geometry and trigonometry to explain their shadows and length and duration of eclipses; and gives several algorithms to calculate, predict, eclipses, star-planet conjunctions etc. Surya Siddhanta is explained as the revelation of astronomy by Surya Deva to an asura called Maya; very similar to the revelation of Vedas to the rishis during their meditations. So the spherical model was conceived, propagated and accepted among astronomers before composition of Surya Siddhanta. The other siddhantas compared by Varahamihira also don’t seem to have any explanation.

Was sphericity an idea borrowed from Greeks? It is plausible, maybe even probable. European writers assume they are, without bothering to prove so. Did the Greeks borrow the idea from the Babylonians? Again possible, but European writers don’t even mention this possibility. Can we completely rule out the possibility that Indians did not discover it on their own? No. Greek and Roman astronomers were well respected, as Varahamihira states. Romaka (name afted Rome or Roma) and Paulisa probably Paulus Alexandrinus of Alexandria, are among the 18 rishis to whom their eponymous siddhantas are attributed. But there are no books in the Greek language attributed to them. A lot of astronomy and mathematics attributed to Greeks like Ptolemy, Archimedes and Euclid are not found in Indian astronomy.

Rotation and Refutation

Aryabhata asserted that the earth rotates and the stars only seem to revolve around it. He used a metaphor for this also: just like a passenger in a boat on the Ganga feels like the trees on the shore are moving backward, rather than that the boat was moving forward, he said, so does the earth rotate from west to east, but people feel as though the sky and stars rotate westward.

This assertion, was dismissed not only by Brahmagupta and Varahamihira but even by his ardent admirers and commentators through the succeeding centuries. Perhaps because he was only a man, not a rishi – hence his composition was only a manuja grantha.

If Aryabhata’s rotation theory were correct, countered Varahamihira, in Pancha Siddhantika, Chapter 13, how would any falcon or other bird ever return to its nest? For the earth would have moved a great distance while the bird was flying. Flags would always stream westward due to the wind produced by the very fast moving earth. If the refutation was that earth moves slowly, how would it revolve such a great distance within a day? Varahamihira stated that the earth’s circumference is 3200 yojanas, about 25,000km as a yojana is 8km.

Someshvara, an eighth century commentator of Aryabhatiyam, went much further. If the earth revolved, he said, oceans will flood all the lands, and tops of trees and castles woud be blown away by the storm of the wind caused by such a ferocious speed of rotation. So, he concluded, the earth does not rotate.

So they didn’t understand inertia, or frame of reference for motion. But given the facts and theories at their disposal, these were scientific rejections of Aryabhata’s conjecture, not superstitious or theological objections. This is only discernible to those who study all the original material; most accounts make it seem that Aryabhata’s rotation conjecture was scientific and the others stubborn and unscientific in their rejection.

Historically, this is similar to Lord Kelvin’s rejection of Darwin’s theory of Evolution, which dated life on earth to 500 million years. Kelvin, calculated that the Sun composed of Hydrogen, could have a maximum life of only 300 million years based on chemical combustion of hydrogen to produce heat. The Sun’s true age was confirmed with Einstein’s mass-energy equivalence, nuclear physics, Bohr’s atomic model and such associated phenomena in physics (nothing in biology).

Aryabhata’s rotation conjecture is untenable without a theory of intertia and Newtonian or even Cartestian gravity. Darwin’s age of earth and life predictions were untenable without a nuclear theory of the Sun’s heat generation and subsequent long age of Sun and Earth.

Further Aryabhata and all other Indian astronomers, stated that the entire celesital sphere, gruhams and nakshatram, revolve around the earth from East to West, propelled by a celestial wind called pravaha. Here Aryabhata seems to contradict himself. Either the earth rotates and therefore it appears that stars  revolve; or the stars revolve, with no need for the earth’s rotation. Can he have both?

Varahamihira’s simple metaphor seemed to suffice for Indian astronomers. I wonder if European, Arab  or Chinese astronomers  gave a similar metaphor to explain away spherical earth.

Consequences of the Spherical Model

The spherical model of the earth led to the realization that shadows of the moon and earth cause eclipses. Varahamihira gave a clear explanation of how and why this happens, with an explicit refutation of the Rahu story (see link below).

Sphericity was important, perhaps even more so, than gravity. The development of geometry and triogonometry and understanding about the regularity of planetary orbits, culminated in the ability to predict eclipses; and later star-planet conjunctions. India led the world for a thousand years in this field because of this.

This is also why Lord Napier, a governor of Madras presidency, came to India to write a history of Mathematics, because he thought India was the birthplace of mathematics. It is notable that he was the descendant of John Napier, who invented Logarithms.

They also set Ujjain as the locus of the Prime Meridian (a role now played by the Greenwich Meridian) and all Indian astronomical calculations were based on the Ujjain meridian or at the point where the Ujjain meridian crossed the Equator.

There is an inherent understanding that both the equator and Ujjain meridian would be each be zero degree – something only Indians could use, having invented the zero. Arabs borrowed this zero a few centuries after Aryabhata (around 850 AD, during the time of Abbassid Caliph al Mamun) and Europeans mainly via Leonardo Fibonacci, a Venetian businessman who learnt it from visiting Baghdad in the thirteenth century. But the Ujjain meridian precedes Aryabhata and Varahamihira, as it is a fundamental factor in the Rishi Siddhantas.

It is an atrocity that these basic scientific concepts, Indian discoveries to be proud of, are not in our school or college books, and that most Indian scientists are unaware of these. These are low hanging fruit.

Related Essays

Varahamihira’s eclipse proof

My essays on Astronomy

Tamil podcast on Varahamihira

Update 10 July 2025 Here is the YouTube link for my lecture Sphericity and its consequences, where I explain adoption of spherical model of earth and its mathematical and astronomical consequences 

This is the YouTube link for an earlier lecture Moon Rise to Masala Dosa

 

Indian Science Festival - Hyderabad

I will deliver a talk titled "Varahamihira's Eclipse Proof" at the Indian Science Festival, Hyderabad, at 11am this Saturday 21st January 2023. At Nucleus Arena.

Entry is free to public. Click here for Registration, schedule  

I will also conduct a workshop on Aryabhata's square/cube roots algorithms at 12pm on Sunday January 22. Limited seats. 

Addendum Feb 24: I wrote an essay summarizing some of what I heard at ISF, Hyderabad and it was published in SouthFirst magazine. Read it here!

In 2020, Badri Seshadri and I presented talks on Indian Mathematics titled The Men who knew Zero to Infinity at ISF Pune. Video links are below:

Part 1 : R Gopu

Part 2 : Badri Seshadri

Brhat Samhita - 7 - Ten books that influenced me

I stumbled upon Indian astronomy. And Varahamihira.

In 2004, I attended a series of weekend talks conducted by Dr Devadoss, an astronomer of Chennai, at the Birla Planetarium, Kotturpuram. It was about astronomy in general, but he mentioned the twenty seven stars in the Indian almanac and enumerated their English and Latin names. For the first time, the idea that India had a long and hoary history in astronomy that I was completely unaware of, struck me. But I didn't pursue it then.

At a series of talks by Dr Chitra Madhavan, on Indian history, at the Musiri house, I encountered Prof Swaminathan, who later gave a series of talks on the Oral Traditions of Sanskrit. This was a eye-opening, mind blowing, paradigm altering experience, as profound and as transformative as reading Sivakamiyin Sabatham or visiting Ellora.

Later I came to know that Prof Swaminathan and others were conducting a series of talks under the banner of Tamil Heritage Trust. He invited me to participate in a discussion about what other programs we could conduct. While others suggested Indian art, sculpture, painting, with such themes as Ajanta, Hampi, Tanjavur etc. I suggested Indian science, particularly astronomy.

"Wonderful", said Prof Swaminathan. "You give a talk on Indian astronomy". And he gave me a book titled Facets of Indian Astronomy by KV Sarma. Around this time, the mathematician and polymath N Balasubramanian (known to aficionados of tamil fiction as short story writer Nagupoliyan) announced he would start teaching Sanskrit. He had also attended Swaminathan's Oral Traditions lecture series at Badri Seshadri's invitation.

My father got suddenly ill and died around that time, on October 5, 2010. My astronomy lecture was scheduled for November 2010.

Preparing for the talk on Indian astronomy helped occupy my mind. Eerily, my father himself had to go to court regularly following my mother's death in 1981, and I suspect work helped abate the grief. For me also, preparing for this lecture, was a way to help dull the grief of my father's passing.

I searched for and stumbled upon several websites about the astronomy and mathematics of other ancient cultures during this time. My plan was to have a ten minute preamble about the Astronomy of Ancient cultures but I learnt a ton of stuff. Prof Swaminathan suggested that I turn it into two lectures, the first on ancient astronomy of other civilizations; the second on Indian astronomy. Which I did.

My first talk on Astronomy of Ancient Cultures went fine, if somewhat long, to a limited but attentive audience, with Deepavali fireworks exploding all around us. The second talk was postponed twice, to February, to accommodate Kathie Brobeck and Blake Wentworth, American speakers who were visiting India at that time.

In the meanwhile, my friend VSS Iyer gave me the soft copies (PDF files) of translations of ancient Sanskrit texts including Aryabhata's Aryabhatiyam, VarahaMihira's Brhat Samhita and Pancha Siddhantika, Bhaskara's Siddhanta Sironmani; and Surya Siddhanta. The Sanskrit classes of Balu sir were going along, and I visited the KV Sarma Library a couple of times with him. Balu sir, as a Sanskrit scholar and mathematician, had a deep interest in and knowledge of mathematics and astronomy in Sanskrit. He also personally knew KV Sarma and had interacted with him over the decades. He was well known among the Sanskrit/mathematics circle, especially by Dr Mamata Dash and Dr Sinirudhdha Dash, who were shishyas of KV Sarma, and then and now run the KV Sarma library and foundation.

And so I had a little more time to read the Sanskrit books and their translations at leisure. The mathematics and astronomy were in Aryabhata were delightful, if cryptic and confounding even for Balu sir. But the polymath Varahamihira is the one who struck a chord.

Especially his mangum opus Brhat Samhita. 

This was more about astrology than astronomy; but it really seemed to be about everything that Varahamihira could see or feel, on earth, not just in the sky. There were chapters on various planets. 

No surprise, right? But also a chapter on Comets. Oddly, no other classical Indian astronomer discussed them. A chapter on planetary conjunctions. Rain. The star Canopus (Agastya). The consellation Ursa Major (Sapta Rishi).

Then it got freaky. A chapter on Diamonds, pearls, rubies. Chapters on Cots; Seats; umbrellas. Perfumes. Pimples. Temples.

Cows, dogs, turles, horses, elephants. Rainbows, dust storms, thunderbolts. Commodities and their prices.

Who else in the world could discuss pimples, temples, thunderbolts and planetary conjunctions in one single book?!? Not even Isaac Asimov. No wonder al-Beruni was flummoxed by Varahamihira, in a way no other he was not by any other Indian jyotisha.

The chapter on Agastya is the one that pulled me in hook line and sinker. Ten beautiful poems, extolling and adoring Agastya in marvelous metaphors and imagery, not distinguishing between the rishi and the star.

The crowning touch was a chapter whose English title is "On the praise of Women" (Stree prashamsa). It may drive any modern feminist into a wordless fury, and probably drove Vatsyayana to jealous sighs. One suspects that Chidambaram Iyer, the translator was very tentative in the translation of this chapter, especially the last shloka about the actions of Shiva, when the apsara Tilottamma came to worship Shiva and Parvati.

Another interesting aspect was his eclipse proof, in a chapter titled Rahu-chaara, which I have explained in this essay. 

While the astronomy and mathematics in other Sanskrit books enthrall and delight with me their knowledge of and explanation of science and mathematics, it is the polymath spirit of Varahamihira and his unabashed delight in life and exposition as a rasika in Brihat Samhita, that captured my heart. And taught me, along with Richard Feynman and Alfred Russel Wallace, not to look at science drily and in detachment, but with delight and pleasure.

Related Links

Literature essays in my blog

Astronomy essays

KV Sarma Library and Foundation

வராகமிஹிரரின் கிரகணச் சான்று

The English version of this essay is here

வராகமிஹிரர் – அறிவியல் மேதையா, பழைய கர்ணாடகமா? விவாதிக்க வேண்டிய கேள்வி. மகாராஜாக்களில் ஆரம்பித்து மாடு, குரங்கு வரை சகல ஜீவராசிகளின் தலையெழுத்தையும் கிரகங்கள்தான் நிர்ணயிக்கின்றன என்று வகுத்து சொன்ன வராகமிஹிரரையும் ஒரு மோசமான கண்கட்டி வித்தைக்காரர் என்றுதான் ஒதுக்க வேண்டியிருக்கும்.அவரும் மூட நம்பிக்கையில் மூழ்கிப்போன ஜோதிடரில் ஒருவர்தானோ?

எதையும் அறிவியல் கண்ணோட்டத்தோடு பார்த்து பழகி, வியந்து பாராட்டும் சமகால வானியல் மற்றும் கணித ஆர்வலர்களைப்போல் நானும் ஆர்யபடரையும் பாஸ்கரரையும் மட்டும் புகழலாம். அவர்களது நுண்ணிய கணித சூத்திரங்களில் நெகிழலாம். வராகமிஹிரரைஒரு ஜாதக பட்டிக்காடு என்று நமட்டு சிரிப்புடன் ஓரங்கட்டி அவர் இயற்றிய பஞ்சசித்தாந்திகத்திலும், பிரிஹத் சம்ஹிதையிலும் செய்தவற்றை பித்தலாட்டம் என்று பகடி செய்யலாம்.

இந்திய வானியலை, குறிப்பாக ஜோதிடத்தின் மீதான நம்பிக்கையை குறை கூறி, அறிவியலை உயர்த்திப்பிடித்து பேசுவதற்கு ஒரு வாய்ப்பு கிடைத்த்து. நான் மறுத்துவிட்டேன். எனக்கு ஜோதிடத்தில் நம்பிக்கை இல்லை. ஆனால் ஜோதிடத்தை நம்புவோரை காயப்படுத்துவதில் விருப்பமில்லை (நையாண்டி செய்வேன்; அது வேறு). நான் புரிந்து கொண்டதை, மற்றவர்களோடு பகிர்ந்து கொண்டு, அதன் மூலம் சிலருக்கு இத்துறையில் ஆர்வம் பிறந்தால் சந்தோஷம்.

வராகமிஹிரர் சர்வ நிச்சயமாக ஒரு முழுமையான இந்திய வானியலாளர் என்று சொல்ல முடியும். வானியலில் அவரது அசாத்திய பங்களிப்பை வைத்தே இதை முடிவு செய்துவிடலாம். வராகமிஹிரர் எழுதிய ப்ரஹத் சம்ஹிதா, விரிவான ஒரு ஒரு கலைக்களஞ்சியம். சுருக்கமான விவரணைகளுக்கு பிரசித்தி பெற்ற ஆர்யப்படரின் ஆர்யபடீயம் எனும் ஆர்ய அஷ்டஷதம் போன்றதல்ல இது.

வராகமிஹிரர் வாழ்ந்த காலத்தில் புகழ்பெற்றிருந்த ஐந்து முக்கியமான வானியல் நூல்களை (சித்தாந்தங்களை) ஒப்பிடும் நூலே பஞ்ச சித்தாந்திகை. ஆனால் அவரது சம காலத்தில் வாழ்ந்த ஆரியபடர் இயற்றிய ஆரியபடீயம் இத்தகைய ஐந்து சித்தாந்தத்தில் ஒன்றல்ல!

ஆரியபடீயமே இன்றுவரை அதிகளவில் விவாதிக்கப்பட்ட, மொழிபெயர்க்கப்பட்ட இந்தியப் புத்தகமாககருதப்படுகிறது. அதில் சொல்லப்பட்ட சூத்திரங்களும், நெறிமுறைகளும் காலாவதி ஆனபின்னரும் பதிநான்காம் நூற்றாண்டுவரை ஆரியபடத்திற்கு பல விளக்க உரைகள் எழுதப்பட்டன. அதில் சொல்லப்பட்டவற்றில் சில விஷயங்கள் தவறென்று நிரூபிக்கப்பட்டிருக்கின்றன. ஒருசில விஷயங்கள் பின்னாளில் மேம்படுத்தப்பட்டிருக்கின்றன.

விஞ்ஞானப்பூர்வமான அணுகுமுறைக்காக ஆர்யபடர் கொண்டாடப்படுகிறார். ஆனால் ஆர்யபடரின் விவரணைகளில் எந்தவொரு வலுவானசான்றும் நிரூபணமும் இல்லை. ஓரிருவரை தவிர, அவருக்குப் பின்னர் வந்த இந்திய வானியலாளர்களும்  விஞ்ஞான ரீதியாக விளக்குவதற்கு முயற்சி செய்ததில்லை. ஒருவேளை தங்களுடைய மாணவர்களுக்கு மட்டும் சொல்லித் தரப்பட்டு, நூலாக எழுதப்படாமல் விடப்பட்டிருக்கலாம். கணித்த் துறையின் தேற்றங்களும் நிரூபணங்களும் கிரேக்கத்தின் கொடை என்றே சொல்லவேண்டும். 

இந்நிலையில் வராகமிஹிரரின் கிரகணச் சான்று, நண்பகல் சூரியனைப் போல் பிரகாசிக்கிறது.அவரது ப்ருஹத் சம்ஹிதையில் வர்ணித்துள்ள கிரகணச் சான்று,  பாமரனாலும் புரிந்து கொள்ள முடியும். கிரகணம் என்னும் மூடநம்பிக்கைகளில் தொலைந்து போன ஒரு வானியல் அற்புதத்தை விஞ்ஞானப்பூர்வமாக விளக்கியிருக்கிறார்.

கிரகணம் என்பது ராகு, கேது பாம்புகள் சம்பந்தப்பட்ட புராணக்கதை என்பதல்ல. பூமியின் நிழல் சந்திரன் மீது விழுவதாலும், பூமிக்கும் சூரியனுக்கும் நடுவே சந்திரன் வருவதாலும் நிகழும் நிழல்களின் விளைவே. இதைத்தான் வராகமிஹிர   ர் தர்க்க ரீதியாக விளக்கியிருக்கிறார். பின்னர் வந்த பிரம்மகுப்தர், தன்னுடைய முன்னோடிகளான ஆர்யபடரையும் விஷ்ணுசந்திரரையும் சலிக்காமல் வெளுத்துவாங்கினார். குட்டினாலும் மோதிர குட்டு; திட்டினாலும் இலக்கிய திட்டு என்பார்கள். அதுபோல் அல்லாமல் இயல்பான நடையில், யாரையும் பழிக்காமல், மரபையும் இழிக்காமல் கூறியிருப்பதுதான் வராகமிஹிரரின் சிறப்பு.

ராஹுசாரம் என்னும் பிரிவில் வரும் ஒரு சில ஸ்லோகங்களை இங்கே மேற்கொள் காட்டியிருக்கிறேன். வடிவியல், திசை, நேரம், அளவு மாறுபாடு ஆகிய நான்கு காரணிகளை அடிப்படையாக வைத்து கிரகண நிகழ்வை விளக்கும் ஸ்லோகங்கள் இவை.

वृक्षस्य स्वच्छाया यथैकपार्श्वे भवति धीर्घचया।

निशिनिशि तद्वद्भूमेरावरणवशाद्दिनेशस्य॥

வ்ருʼக்ஷஸ்ய ஸ்வச்சா²யா யதை²கபார்ஸ்²வே ப⁴வதி தீ⁴ர்க⁴சயா |

நிஸி² நிஸி²தத்³வத்³ பூ⁴மேராவரணவஸா²த்³ தி³னேஸ²ஸ்ய ||

பதம்பிரிப்பு வ்ருʼக்ஷஸ்ய (விருட்சத்தின்) ஸ்வச்சா²யா (சொந்தநிழல்) யதா²(எவ்விதம்) ஏகபார்ஸ்²வே (ஒருபக்கம்) தீ⁴ர்க⁴சயா(நீளநிழல்) ப⁴வதி(ஆகிறதோ)

நிஸி²நிஸி²(இரவுக்கிரவு) தத்³வத்³(அவ்விதம்) பூ⁴மே(பூமியின்) ஆவரணவஸா²த்³(மூடுகிறது) தி³னேஸ²ஸ்ய (சூரியனுடைதை)

பொருள் விளக்கம் ஒரு மரத்தின் மீது சூரிய ஒளி படும்போது, மறுபக்கம் மரத்தின் நிழல் விழுகிறது. விழும் நிழலானது, மரத்தை விட அளவில் பெரிதாக இருக்கிறது. அதே போல் சூரியனின் வெளிச்சம் படும்போது பூமியின் நிழலும் அண்டவெளியில் வீழ்கிறது. என்னவொரு எளிமையான, ஆழமான விளக்கம்.

भूच्छायां स्वग्रहणे भास्करमर्कग्रहे प्रविशतिन्दुः।

प्रग्रहणमतःपश्च्चान्नेन्दोर्भानोश्चपूर्वार्द्धात्॥

பூ⁴ச்சா²யாம்ʼ ஸ்வக்³ரஹணே பா⁴ஸ்கரமர்கக்³ரஹே ப்ரவிஸ²திந்து³​: |

ப்ரக்³ரஹணமத​: பஸ்²ச்சான்னேந்தோ³ர் பா⁴னோஸ்² ச பூர்வார்த்³தா⁴த் ||

பதம்பிரிப்பு பூ(பூமி) சா²யாம்ʼ(நிழலை) ஸ்வக்³ரஹணே (தன்கிரகணத்தில், அதாவது, சந்திரகிரகணத்தில்) பா⁴ஸ்கரம (சூரியனை, அதாவதுசூரியனின்பிம்பத்தை) அர்கக்³ரஹே (சூரியகிரகணத்தில்) ப்ரவிஸ²த் (நுழைகிறது) இந்து (சந்திரன்)

ப்ரக்³ரஹணம(கிரகணம்) அத:(அதனால்) பஸ்²ச்சாத்(மேற்கிலிருந்து) ந(இல்லை) இந்தோ³(சந்திரன்) பா⁴னோ(சூரிய) ச(மற்றும்) பூர்வார்த்³தா⁴த்(கிழக்கிலிருந்து)

பொருள் விளக்கம் சந்திர கிரகணத்தின்போது பூமியின் நிழல் விழம் பகுதிக்குள் சந்திரன் பிரவேசிக்கிறது. அதே போல் சூரிய கிரணகத்தின்போது, சூரியனின் பிம்பவட்டத்தில் சந்திரன் பிரவேசிக்கிறது. ஆகவே சந்திர கிரகணம் மேற்குப்பகுதியில் ஆரம்பிப்பதில்லை. அதே போல் சூரிய கிரகணமும் கிழக்குப் பகுதியில் ஆரம்பிப்பதில்லை.

சந்திர கிரணகத்தின் போது கிழக்கிலிருந்து மேற்காகவும், சூரிய கிரகணத்தின்போது மேற்கிலிருந்து கிழக்காகவும் கிரகணங்கள் நிகழ்வதை திசைகளை அடிப்படையாக வைத்து விளக்குகிறார். சந்திர கிரகணம் கிழக்கிலிருந்து மேற்காக நிகழ்கிறது. சூரிய கிரணகத்தின்போது, மேற்கிலிருந்து கிழக்காக சந்திரன் பூமியை மையமாக வைத்து சுற்றிவருவதால் சூரியனின் மேற்குப்பகுதியிலிருந்து கிரகணம் ஆரம்பிக்கிறது. 

आवरणंमहदिन्दोः कुण्ठविषाणस्ततोऽर्द्धसञ्छन्नः।

स्वल्पं रवेर्यतोऽतस्तीक्ष्णविषाणो रविर्भवति॥

ஆவரணம்ʼ மஹதி³ந்தோ³​: குண்ட²விஷாணஸ்ததோ (அ)ர்த்³த⁴ஸஞ்ச²ன்ன​: |

ஸ்வல்பம்ʼ ரவேர்யதோ(அ)தஸ்தீக்ஷ்ண விஷாணோ ரவிர் ப⁴வதி ||

பதம்பிரிப்பு ஆவரணம்ʼ(மூடுவது) மஹத்³(பெரிது) இந்தோ³​: (சந்திரனை) குண்ட²(மொக்கை) விஷாண(கொம்பு) ததோ(ஆதலால்) அர்த்³த⁴ ஸஞ்ச²ன்ன​: (பாதிமூடியுள்ளது)

அல்பம்ʼ (சிறிது) ரவே (சூரியனின்) யதோ (ஏனெனில்) அத: (அதனால்) தீக்ஷ்ண (கூர்ந்த) விஷாணா: (கொம்புகள்) ரவி:(சூரிய) ப⁴வதி(ஆகிறது)

பொருள் விளக்கம் சந்திரனை விட பூமியின் உருவம் பெரிதாக  இருப்பதால், கிரகணக்கொம்புகளின் விளிம்புகள் தெளிவாக இருப்பதில்லை. அதே சமயம், சூரியனை மறைக்கும்போது சந்திரனின் உருவம் சிறியது என்பதால், கிரகணக் கொம்புகளின் விளிம்புகள் பளிச்சென்று தெரிகின்றன.

சூரியன், சந்திரன், பூமி ஆகிய மூன்றும் வெவ்வேறு அளவுள்ள கோள்கள் என்பதை அடிப்படையாக வைத்து சொல்லப்பட்ட விளக்கம். சூரியனையோ, சந்திரனையோ மூடும்போது வெளிப்படும் வட்டத்தின் ஓரப்பகுதியை கொம்புகள் என்கிறார் ஆசிரியர். படத்தில்காணலாம் – முக்கால்வட்டம் நிழலிலிருக்க, சிவப்பாய் தெரியும் பகுதி மாட்டுக் கொம்பை போல் உள்ளதால் கொம்பு என்றே அழைக்கப்படுகிறது. குண்டவிஷானா, தீக்ஷனவிஷானா என்பவை சமஸ்கிருதத்தில் ஜோதிடர் புனைந்த அழகான அறிவியல் வார்த்தைகள். மூன்று கோள்களும் வெவ்வேறு உருவ அளவை கொண்டுள்ளன என்பதை திட்டவட்டமாக இங்கே விளக்கியிருக்கிறார். சந்திரனின் அளவு சிறியது. பூமியின் நிழலோ பெரியது. அளவு மாறாத ராகுவால் விழுங்கப்பட்டால் நிழல்களும் கொம்புகளும் வேறுபடுமா?

சூரியனின் கொம்பு - படம்: விஜய்குமார் (PoetryInStone)

இன்னொரு சுவராசியமான விஷயம். வராகமிஹிரர் கேது என்ற சொல்லை கிரகணத்திற்கு சொல்வதில்லை. தூமகேது என்று, வால்மீனுக்கு மட்டும் சொல்கிறார்.

ராகு என்னும் பாம்பை பற்றிய கதைகளுக்கு பஞ்சமில்லை. ராகுவிற்கு தலையும், வாலும் உண்டு. ராகு ஒரு உருவமுள்ள பாம்பு. கருப்பாக இருக்கும். கிரகண நேரங்களைத் தவிர மற்ற நேரங்களில் கண்ணுக்குத் தெரியாது. இப்படி ஏராளமான கதைகள் உண்டு. சமணர்களின் வானியலில் இரண்டு ராகு உண்டு.

यदि मूर्त्तो भविचारी शिरोऽथवाभवति मणडली राहुः।

भगणार्द्धेनान्तरितौ गृह्णाति कथं नियतचारः ॥

யதி³மூர்த்தோ ப⁴விசாரீ ஸி²ரோ (அ)த²வா ப⁴வதி மணட³லீ ராஹு​: |

ப⁴க³ணார்த்³தே⁴னாந்தரிதௌ க்³ருʼஹ்ணாதி கத²ம்ʼ  நியதசார​: ||

பதம்பிரிப்பு யதி³(ஆகுமாயின்) மூர்த்தோ (உருவம்) ப⁴விசாரீ(வானில்ஊர்பவன்) ஸி²ரோ(head) (அ)த²வா(எனின்) ப⁴வதி(ஆகிறது) மணட³லீ(வட்டத்தை) ராஹு:

ப⁴க³ணார்த்³தே⁴ன (பாதிவானத்தால்) அந்தரிதௌ(இடைவெளிபட்ட) க்³ருʼஹ்ணாதி(கவ்வுவது) கத²ம்ʼ (எவ்விதம்) நியதசார​:(விதிவழிசெல்வோன்)

பொருள் விளக்கம் ராகுவுக்கு உருவம் இருந்தால், தலையை வைத்து அடையாளம் காணமுடியும். விண்வெளியில் எதிரெதிரே இருக்கும் சூரியனையும், சந்திரனையும் கணிக்க முடிந்த நேரத்தில் எப்படி தாவிப்பிடிக்க முடியும்? அதாவது, கணிக்கக்கூடிய வட்டத்தில் மட்டும் பாம்பு ஊர்வது ஏன்?

अनियतचारः खलुचेदुपलब्धिः संख्यया कथं तस्य ।

पुच्छाननाभिधानोऽन्तरेण कस्मान्नगृह्णाति॥

அனியதசார​: க²லுசேது³பலப்³தி⁴​: ஸங்க்²யயா கத²ம்ʼ  தஸ்ய |

புச்சா²னனாபி⁴தா⁴னோ (அ)ந்தரேண கஸ்மான்ன க்³ருʼஹ்ணாதி ||

பதம்பிரிப்பு அனியதசார​:(விதிவழிசெல்லாதான், அதாவதுதன்னிச்சையானவன்) க²லுசேது³பலப்³தி⁴​: (கிடைக்கும்) ஸங்க்²யயா(கணித்து) கத²ம்ʼ(எவ்விதம்) தஸ்ய(அதனை)

புச்சா²(வால்) ஆன்ன(முகம்) அபி⁴தா⁴னோ(பெயர்களை) அந்தரேண (நடுவில்) கஸ்மாத்(எவ்விதம்) நக்³ருʼஹ்ணாதி(கவ்வுதில்லை)

பொருள் விளக்கம் கணிக்கக்கூடிய வட்டத்தில் ராகு ஊர்வதில்லை எனில் கிரகண காலங்களை எப்படி முன்கூட்டியே நம்மால் கணிக்க முடிகிறது? ராகுவுக்கு தலையும், வாலும் மட்டும் இருந்தால், விண்ணில் எதிரெதிராய் சூரியனும் சந்திரனும் இருக்கும்போது மட்டும் கவ்வி, வேரெங்கும் இருக்கும்போது ஏன் கவ்வுவதில்லை?

अथ तु भुजगेन्द्ररूपः पुच्छेन मुखेन वास गृह्णाति ।

मुखपुच्छान्तरसंस्थं स्थगयति कस्मान्नभगणार्द्धम्॥

அத² து பு⁴ஜகே³ந்த்³ர ரூப​: புச்சே²னமுகே²ன வாஸ க்³ருʼஹ்ணாதி |

முக²புச்சா²ந்தரஸம்ʼஸ்த²ம்ʼ ஸ்த²க³யதி கஸ்மான்ன ப⁴க³ணார்த்³த⁴ம் ||

பதம்பிரிப்பு அத²து(ஒருக்கால்) பு⁴ஜகே³ந்த்³ரரூப​: (நாகராஜரூபன்) புச்சே²னமுகே²ன(வாலாலும்முகத்தாலும்) ஸ(அவன்) க்³ருʼஹ்ணாதி(கவ்வுகிறான்)

முக²புச்சா²ந்தரஸம்ʼஸ்த²ம்ʼ (முகத்திற்கும்வாலிற்கும்இடையுள்ளபகுதி) ஸ்த²க³யதி(மூடுவது) கஸ்மாத்(எவ்விதம்) ந(அல்ல) ப⁴க³ணார்த்³த⁴ம்(பாதிவானத்தை)

பொருள் விளக்கம் ராகு ஒரு முழுமையான பாம்பாக இருப்பின் வாயாலும், வாலினாலும் சூரியனையோ சந்திரனையோ விழுங்கும் போதுசூரியனுக்கும் சந்திரனுக்கும் நடுவிலுள்ள அனைத்து விண்மீன்களையும் ஏன் அவன் உடலின் நிழலில் மறைவதில்லை?!

राहुर्द्व्यंयदिस्याद्ग्रस्तेस्तमितेऽथवोदितेचन्द्रे।

तत्समगतिनान्येनग्रस्तः सूर्योऽपिदृश्यते॥

ராஹுர்த்³வ்யம்ʼ யதி³ஸ்யாத்³ க்³ரஸ்தேஸ்தமிதே (அ)த²வோதி³தே சந்த்³ரே  |

தத் ஸமக³தி னான்யேன க்³ரஸ்த​: ஸூர்யோ (அ)பி த்³ருʼஶ்யதே ||

பதம்பிரிப்பு ராஹுர்த்³வ்யம்ʼ(இருராகுகள்) யதி³ஸ்யாத்³(இருப்பின்) க்³ரஸ்தே(கவ்வும்கால்) அஸ்தமிதே(சாயும்காலமோ) அத²வா(அல்ல) உதி³தே (உதிக்கும்காலமோ) சந்த்³ரே(சந்திரனை)

தத்(அந்த) ஸமக³தி(சேர்ந்துசெல்லும்) அன்யேன(மற்றதால்) ந(அல்ல) க்³ரஸ்த​: (கவ்வுவான்) ஸூர்ய:(சூரியன்) அபி(கூட) த்³ருʼஶ்யதே(காணப்படுகிறான்)

பொருள் விளக்கம் இரண்டு ராகு பாம்புகள் இருப்பதாகவே வைத்துக்கொள்வோம். ஒரு ராகு சந்திரனை விழுங்கும்போது, வேடிக்கை பார்ப்பதை நிறுத்திவிட்டு ஏன் இன்னொரு ராகு சூரியனை விழுங்க முயற்சிக்கக்கூடாது?

எந்த அடிப்படையில் பார்த்தாலும் கிரகணங்கள் நிகழ்வது என்பது பாம்பு விழுங்கும் கதையல்லஎன்பதை அழுத்தம் திருத்தமாக நிரூபித்துள்ளார் வராகமிஹிரர்.

வாஸ்கோடகாமாவும் அவரைத் தொடர்ந்து ஐரோப்பியர்களும் இந்தியாவுக்குள் கரையேறும்வரை காகிதம் பற்றி இந்தியருக்கு தெரியாது. அதுவரை காகிதம் சீனாவிலிருந்து இறக்குமதி செய்யப்பட்டதில்லை. 19ஆம் நூற்றாண்டின் தொடக்கத்தில்தான் காகிதம் நம்மூரில் பயன்பாட்டுக்கு வர ஆரம்பித்தது. அதுவரை எழுதுவதற்கு கிடைத்தவை வெறும் ஓலைச்சுவடிகளும், மரப்பட்டைகளும்தான்.விண்ணியலும் கணிதமும் பாடமாக குழந்தைகளுக்கு சொல்லித் தரப்பட்டதில்லை. பண்டிதருக்கும் இவற்றை புரிந்து கொள்வது எளிமையல்ல. வராகமிஹரரின் விளக்கங்கள், விண்ணியல் பண்டிதருக்கு மட்டுமே. ஆகவே,பொதுமக்கள் மத்தியில் பாம்பு விழுங்கும் கதை உயிர்ப்போடு இருந்ததில் ஆச்சர்யம் ஏதுமில்லை.

ஐரோப்பியர்கள் சொல்லித் தந்த பாடத்தையே திரும்பத் திரும்ப பாடநூல்களில் படிக்கிறோம். பெரும்பாலான அறிவியல் ஆசிரியர்களுக்கு சம்ஸ்கிருத அறிவியல் நூல்களின் கருத்துகள் ஏதும் தெரியாது. ஆர்யப்பட்டரை தவிர மற்ற இந்தியவிண்ணியல் பண்டிதர்கள், ஜோதிடம் வகுத்துத் தரும் மூடநம்பிக்கையாளர்களாகவே சித்தரிக்கப்படுகிறார்கள். வைதீக வழிவந்த வராகமிஹிரரால்தான் கிரகணம் குறித்த விஞ்ஞான ரீதியான விளக்கம் தரப்பட்டது என்பது எத்தனை பேருக்குத் தெரியும்?

நீங்கள் அறிவியலில் ஆர்வம் கொண்டவராக இருந்தால் இவற்றையெல்லாம் இளைய தலைமுறையினரிடம் கொண்டு சேருங்கள்.

பிருஹத் ஸம்ஹிதத்தை புரிந்துகொள்ள ராமகிருஷ்ண பட்டரின் ஆங்கில மொழிபெயர்ப்பும், 1885இல் சிதம்பரம் ஐயர் எழுதிய மொழிபெயர்ப்பும் எனக்கு உதவியது. கணிதர் “நகுபோலியன் பாரதி பாலு” பாலசுப்ரமணியனோடு சென்னை அடையாறு கே.வி. சர்மா நூலகத்தில் இதை கலந்து பேசியது மிகவும் உதவியது.

ஆங்கிலத்தில் நான் எழுதியதை சிறப்பாக பொறுமையாக தமிழில் மொழிபெயர்த்த ஆசிரியர் “ரஜினி ராம்கி” ராமகிருஷ்ணனுக்கு நன்றி நன்றி நன்றி. சமீபத்து சூரிய கிரகணத்தின் படம் தந்த சிங்கப்பூர் விஜய்குமாருக்கும் நன்றி.

விண்ணியல் கட்டுரைகள்

வராகமிஹிரரின் அகத்தியர் துதி

கோயில்களில் விண்ணியல் சிற்பங்கள்

சில விண்ணியல் ஸ்லோகங்கள் – பொருள் விளக்கம்

மகாவீரரின் கணித கனிரசம்

சைலகேது

நீலகண்ட சோமசத்துவரின் சிலேடை

VarahaMihira's Eclipse Proof

பாதமியில் ராம்கியும் நானும் - ஜனவரி 2016